ALIGULAC

What rating system do you use?

I developed my own rating system for this site. It relies heavily on the Glicko rating system, with these differences:

• Each player has an overall rating and a rating for each matchup. The overall rating is always the mean of the matchup ratings.
• I don't use approximations for maximising the likelihood function. Instead, I use numerical optimisation algorithms directly.

For the mathematically inclined, there is a very brief technical paper here. I put it together in an hour or so by request, and I'm aware that it's not exactly thorough or easily readable. (WARNING: This paper is outdated after we switched the underlying probability model from normal to logistic. The basic ideas are still valid, however.)

And in English?

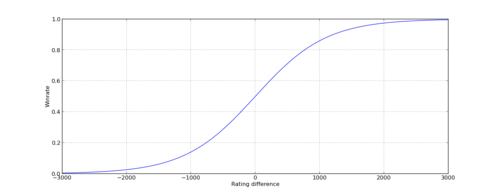
To figure out the probability that a player beats another, take the difference of their relevant matchup ratings, and read out the result from the graph shown. (This is the logistic cumulative distribution function with mean zero and variance 1, scaled by a factor 1000).

Now let's say a player has played a bunch of games during a period and we want to find his new rating. First, we form a likelihood function, which describes how likely a set of outcomes is, given the player's rating. This likelihood function will be a product of such probabilities of the player beating opponent A, B, C... and so on. Now we want to find out which rating maximises this function. That is, which rating maximises the likelihood that the outcomes that happened actually would happen. We also calculate the certainty of the likelihood function at this point. This is a measure of how consistent the results of the given player were in the last period. A high consistency gives a high certainty, and vice versa.

Then, the new rating is adjusted somewhat in the direction of the maximal likelihood rating found above. How much it's adjusted depends on how certain the original rating was, and how certain the maximal likelihood rating is (how consistent the results were). The adjustment will be biased towards whichever of these two is most certain.

Finally, the certainty of the rating is updated. It will always be higher than it was before, reflecting the fact that we now have more information about the player. If the results during the preceding period were very consistent, we will be very certain about his or her rating.

There are some caveats to the above:

• Do not allow the certainty of a player's rating to go above a certain limit. If it does, the system will fail to react to sudden changes in skill.
• If a player only plays games against one race during a period, only the overall rating will change. (That is, the relative matchup ratings will not change). If there are games against two races, the relative matchup rating against the third race will not change.
• If a player has zero losses or zero wins against one or more races, the likelihood function will be maximised only at plus or minus infinity rating, respectively. To avoid this, in these cases I add a fake win and a loss against a hypothetical opponent with the same strength. Thus, if a player goes 0-4 against Protoss, he is effectively treated as having gone 1-5.

How predictive is the system?

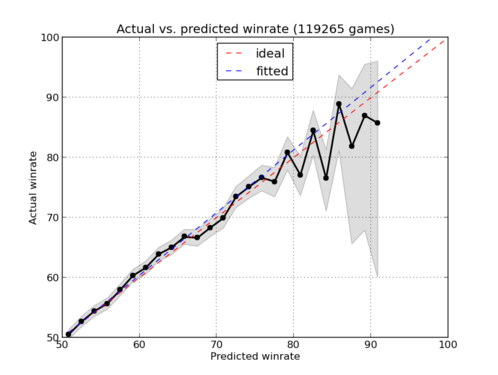
By my understanding, very.

This is a plot of more than 100k historical games (the whole database as of February 2013). On the horizontal axis you find predicted winrate for the presumed stronger player, using the ratings at the time the game was played. The games were grouped in reasonably small groups, i.e. 50%-53.3% and so on upwards. (Obviously no numbers below 50% since this is the predicted winrate for the stronger player.)

On the vertical axis is the actual winrate for each group.

As can be plainly seen, the actual winrate is close to the predicted winrate up to about 80%. The weighted linear fit (blue dashed line) is almost identical to the ideal curve (red dashed line) corresponding to the relationship that predicted winrate equals actual winrate.

Above 80% the winrates become a bit more erratic, and it seems like the system slightly overestimates the chances for the stronger player.

Thus, if the prediction system shows a winrate of

• 80% or higher in a best of 1
• 90% or higher in a best of 3
• 94% or higher in a best of 5
• 96% or higher in a best of 7

the numbers should be taken with a grain of salt.

Why not update in real time?

If I were to update the ratings in real time, first I would have to make some changes to how the algorithm works. Recall that games versus different races are aggregated, and if a player has zero wins or losses, a couple of fake games are added. In real time, such fake games would almost always be required.

Secondly, the discrete nature of time is a way to keep ratings from being excessively volatile. To take the top spot, a player now has to perform well over two weeks, instead of (say) just a couple of days. On the other hand, if the period is too long, the list loses relevance in a quickly-changing pro scene. I ended up compromising with two week periods.

We do, however, update a preview of the next rating list every six hours, so you can see rating changes in something that is close to real time. The system itself is, however, essentially discrete.

Do you weigh games differently?

No, I don't. Korean tournaments and players receive no special treatment. The GSL is difficult because good players play there; the players aren't good because they play in the GSL.

When fitting the model (deciding which parameters to use) I also don't weigh games differently, but this is something we're looking into. Since the database contains an overwhelming majority of non-Korean games, the system will tend to adapt to the non-Korean scene. We've noticed, however, that most people using the service are interested in the Koreans. We are still working on a useful solution to this problem.

You can improve the rating by...

One of the most common forms of feedback we get are about how to improve the rating. These are not bad ideas, they're pretty good, but they might be more complicated than you think. Here are some common ones.

One thing to keep in mind is that a good mathematical model has few parameters. The current rating system has three. Those three parameters are sufficient to give Aligulac the predictive power it has. If you want to suggest complicating the model, the additional parameters must be chosen with care.

Games in regular online tournaments shouldn't count as much as Code S. Well, first we have to realize that games are weighted, in a sense, by opponent skill. You get more points for beating a higher rated opponent than a lower, and you lose more points by losing to a lower rated opponent than a higher. In addition it is worth considering that simply weighing games higher will not automatically increase the rating of those playing. The winners will gain more points, true, but the losers will also lose more. The mean rating of the players playing will not change.

So aside from this, how should this weighing work?

• Even stronger weighing by opponent? The "weighing" is a result of a Bayesian inversion formula depending on the underlying probability model chosen. It's not something that can just be changed, that is, there's no parameter encoding this. It's a much deeper mathematical concept.

• Weighing by mean rating of opponent in a round? Well, why should this be any better than weighing by the actual opponents faced, which is what we already do?

• Weighing by prize pool? The theory goes that strong players are likely to "try harder" if the prize is higher. There is some merit to this idea, but there are also problems. Some tournaments offer prizes in equipment, and not money. Some offer qualification to a higher tier. For example, there is no monetary prize in the GSL Up and Down groups, but nobody would question the incentive to win there. In addition, there are internal team incentives which are not generally public knowledge. And, additionally, if a player knowingly plays weaker in some games, should that not be reflected in the ratings?

• Weighing by tournament? These arguments usually involve some classification of events into tiers of importance with coefficients associated with each level. This approach runs into the complexity problem. With five levels (say), the model becomes far more complicated for what is not shown (yet, anyway) to be reasonable benefit.

• Weighing by online and offline? Yes, this is a legitimate idea and probably the one closest to being implemented. We have working experimental code with this feature already.

Rating gap cap. The idea here is to prevent players from "farming" much lower rated players. It is possible to artificially inflate a player's rating if he never plays other players close to himself in skill. The ideas usually consist of ignoring matches where players are farther away in rating than a given threshold. However, this can be seen as unfair to the lower rated players, who will have their wins against good players discarded. Capping the gap to a given value will make the problem worse. Say a 1700-rated player plays a 1000-rated player, but the cap is 500, so for the purposes of updating the stronger player's rating the lower rated player is assumed to be rated 1200. Then it will be easier for the 1700-rated player to overperform than it was previously.

How do you decide which games to add?

This question doesn't have an easy answer. We mostly decide this on a case-by-case basis. Generally we will add a round from a tournament if that round contains a significant number of already rated players. (Usually higher than 25% or so.) For the large regular cups this usually means somewhere around top 16 to 8.

One common exception to this rule is large national tournaments, which when rated would create a «rating bubble». We try to avoid this as best we can, but it's a difficult thing to do. We are more lenient with tournaments where a significant proportion of the participants regularly compete internationally (Korea, Germany, Poland and Sweden), or if the tournament is significant in another way (such as TeSL).

If a tournament isn't in the database, it could either be because we felt it didn't cut it, or it could just be we have missed it or forgotten. This work is done on a voluntary basis, after all. You could try asking us about it, or submitting it yourself.

The best way for the up-and-coming player to get an Aligulac rating is probably to play lots of open tournaments and LANs, and keep going at it until you reach a round with a fair number of notables.

People are vanishing from your lists

If a player has not played any games for four periods (eight weeks, or about two months), he or she is removed from the list. The entry is still there, and will be taken into account if the player plays a new game some time in the future. It's only kept from the published list to keep it from filling up with uncertain and possibly irrelevant data.

The same happens if your rating uncertainty goes over 200.

I'm aware that a strict limit of only two months may seem harsh, but as the game is so volatile, if a player doesn't play fairly frequently, the ratings quickly become very uncertain and useless. Remember, your rating is still there.

How do the races OP/UP work?

On the period list you can see OP/UP fields, and in the infobox for each period, the same data is given as "leading" and "lagging" race. This is an indicator showing which races are most and least prominent near the top of the list. Specifically, for each race imagine a hypothetical player with a rating equal to the mean of the ratings of the top five players of that race, and imagine these three players playing very many games against each other. If the players were of equal strength, each of them would score about 50%, however, in reality, one of them may score, say, 10% more than that. The race that scores the most in this scenario is the "OP", or "leading" race, and the race that scores the least is the "UP", or "lagging" race.

This is provided as a way to analyse the metagame shifts near the top of the skill ladder, and should not be taken as actual evidence for real game imbalance.

Rating adjustments

The rating adjustments can seem a bit off. Why is that?

Common complaints include players gaining or losing points when they score exactly as expected, or gaining points when they underperform, and losing points when they overperform.

Several things can impact this. First of all, the expected scores are rounded to one decimal place, so you're not seeing the whole story. (An expected score of 1.0–0.0 could in reality be 0.96–0.04 for example.)

Also, you should keep in mind that the rating adjustments for each of the four categories (general rating, and each matchup rating) are not done independently of each other. The system will try to update each rating according to the certainty bias (mentioned earlier), but it's also restricted by the fact that the matchup ratings must have mean equal to the general rating.

The upshot of this is that if a player overperforms versus Terran (say 2–0 when 1–1 was expected), but significantly underperforms in the other matchups (say 0–10 in each when 5–5 was expected), the rating versus Terran may still decrease.

Why is my favorite player not predicted to win?

This could be due to several reasons.

• He just isn't as good as you think he is.

• He hasn't played enough games for the system to recognize that he is good yet. Remember that ratings change strictly on the basis of results, not the manner of games. A shoddy win with plenty of mistakes will earn as many points as a sick timing exploit that leaves the audience breathless.

• Your opinion of your favorite player is clouded by titles and hype. One advantage of a purely objective system like this is that it is immune to the cognitive biases that so often affect humans.

Why is the heaviest favourite not predicted to win?

What people sometimes see when predicting single elimination brackets is that the player with the largest probability of winning is not predicted to win in the median results section.

The reason this happens becomes clear with a small thought experiment. Suppose a player called Alan has a rating of 2000 and he finds himself on one side of a 16-man bracket together with seven other players rated 1999. On the other side of the bracket only one player showed up (Brian). He is also rated 1999, and now he has a bye all the way to the finals.

So who is most likely to win this tournament? Is it Brian or Alan? Well, it's Brian actually. He has a 50% of beating any of the seven 1999-rated players that could come out of Alan's subbracket, and he has a slightly smaller probability (49.X%) of beating Alan, if he wins. So overall Brian's chances of winning are slightly less than 50%. On the other hand, Alan has to win four matches where he is the slight favourite in each of them. That amounts to a probability of slightly more than 12.5%. So clearly Brian is most likely to win.

The way the median results work, however, is to take the least surprising result in each match. Since Alan is favoured against each player he meets, the least surprising result for each match he plays is that he wins. Thus, the median result is that Alan wins the tournament by narrowly edging out each match he plays.

In summary, you can see such discrepancies if the distribution of skill on both sides of the brackets are uneven. The example above was extreme, but this is not such an uncommon phenomenon.

I would definitely recommend to pay more attention to the probabilities than the median results if you are unsure.

Do you need help?

Probably, or at least, depending on what you can offer.

Design: I am a mathematician, and not a web designer. (Maybe you've noticed.) Building this rudimentary site took me longer than I care to admit. I prefer to keep it simplistic, but I wouldn't mind having someone who actually knows what he or she is doing.

Data: At the moment I'm aggregating game results from several other sources. I would love to have an army of volunteers who submitted results directly to my database so that I could keep it up to date without relying on third party websites. I have functionality that allows people to enter results and make new players if needed. Let me know if you are willing to offer a hand, and I'll give you an account!

If you have input, please let me know: evfonn(a)gmail(dot)com.

How do I pronounce "Aligulac"?

The name Aligulac is derived from that of the Roman emperor Caligula, so if you can pronounce that, all you have to do is shift the C to the end and you're good to go.

Here is a decent video demonstrating how to say "Caligula". Personally I use a hard U instead of a soft one (i.e. U as in RUDE instead of YU as in YUSSUF), but I'm not picky.